この難問、あなたは解けるか！？ - 『生き抜くための高校数学』 part 7 「2.3 集合と論理」
どうも、のび作です！
今回は集合と論理。この辺は数学の中でも興味を持っておられる方が多い分野ではないでしょうか。僕も好きなとこです。
クイズ感覚で楽しんでいただければ！
part 1 はこちら
part 6 はこちら
2.3 集合と論理
ある条件の集まりを集合といいます。ただし、ハンサムな男性の集合とか可愛い子犬のような、人によって解釈が異なる集合は集合の対象とはしません。
不意にくるお茶目な言葉がいい感じですね（笑）
ここは言葉の定義が目白押しで中々本題に入れないのが歯がゆいところですが、個人的には、高校数学の中でもっとも生活に役立ち、もっとも面白い箇所といっても過言ではないと思います。
しっかり理解するためにも、こういう基本部分はしっかり押さえていきたいですね。
ざっとまとめてみました。
文字でみるとややこしい気がしなくもないですが、図にするとなんてことないですね。
例１
※途中式は計算速度を優先してこういう書き方をしましたが、実際は「集合＝要素の数」ではないので、そこだけご了承いただければ。
さて、次は論理です。まずは言葉の定義から。
集合と似てますね。
例２（必要条件、十分条件、必要十分条件）
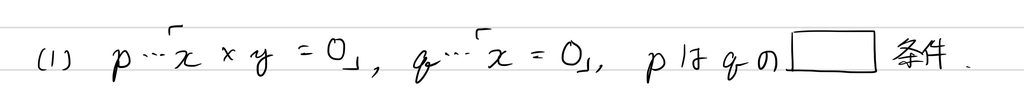
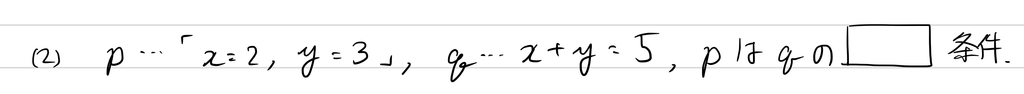
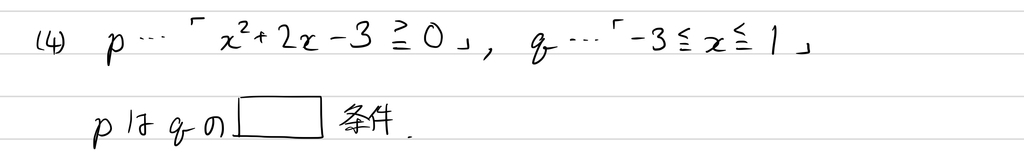
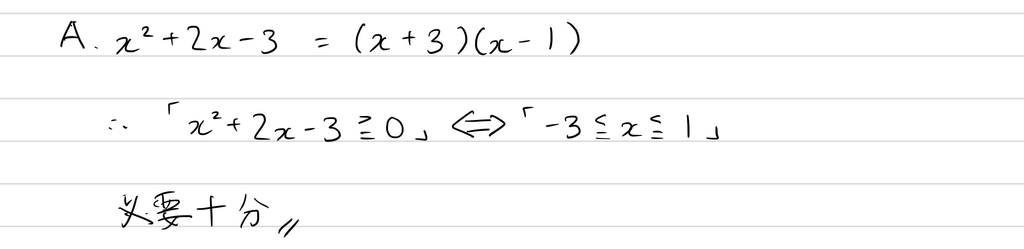
次に、逆、裏、対偶について。ここは著者に何か以前思うところがあったのか熱く語られていますが、図を見れば一発だと思います。
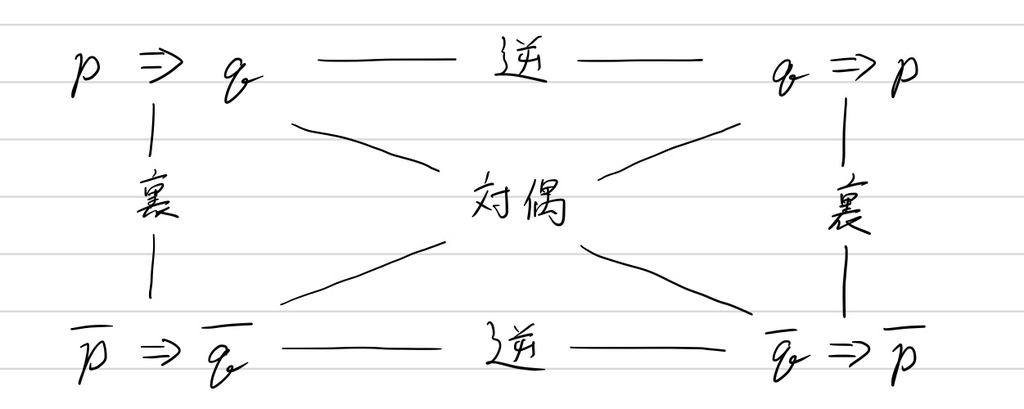命題が成り立つ時、対偶だけは必ず成り立つというところだけ押さえておけばいいかなーと思います。
例３
さて、次は否定文に関して興味深い言及がなされています。
普通に考えると、否定文は「必ずしもどちらかに入っているわけではない」としてしまいそうですが、数学の立場ではこうなるよーということですね。
このようにして次の否定文を考えてみます。
（ア）クラスのすべての生徒は、数学Ⅱを履修している。
否定文「クラスのある生徒は、数学Ⅱを履修していない」
（イ）クラスのある生徒は、身長が190cm以上である。
否定文「クラスのすべての生徒は、身長が190cm未満である」
（ウ）次回の会議が25日に行われるならば、その会議にA氏は出席する。
否定文「次回の会議が25日に行われ、かつその会議にA氏は出席しない」
（ウ）がちょっと難しいかもしれませんね。25日に会議が行われない場合については何も言っていないため、否定でもなんでもなくなってしまうというわけです。
次は例題。ぜひクイズ感覚で解いてみてください。
例題４（否定文）
（１）「自然数nは、3と5の両方の倍数である」の否定文「自然数nは、3の倍数ではないか、または5の倍数でない」
「自然数nは3の倍数でもなく、5の倍数でもない」
「クラスのある生徒は携帯電話をもっていない」
「クラスのすべての生徒はバイクの免許をもっていない」
「プールの水温が25℃以上なのに泳がない」
（５）が一発でできた方は論理学の才能があると言っていいんじゃないでしょうか。
最後に恒等式の説明がでてきました。ここで恒等式の説明がくるとは思いませんでした。
これが同じである、と言っているんですねー。その考え方は目から鱗でした。
「高校数学の段階で、『すべて』と『ある』の用法をマスターすれば、大学の微分積分学や線形代数学は簡単である」
論理学って、数学の中でも他との結びつきが薄い孤高の分野のようなイメージがあったのですが、むしろ他とつながりの強い、優秀な基礎といえそうですね。興味深い。
微積分や線形代数とどう繋がってくるのか、今後注目していきたいところです。
生き抜くための高校数学: 高校数学の全範囲の基礎が完璧にわかる本
- 作者: 芳沢光雄
- 出版社/メーカー: 日本図書センター
- 発売日: 2016/09/17
- メディア: 単行本
- この商品を含むブログを見る
